The ejection of matter in the close vicinity of a young stellar object is investigated, treating the accretion disk as a gravitationally bound reservoir of matter. By solving the resistive magnetohydrodynamic (MHD) equations in two-dimensional axisymmetry using our version of the Zeus-3D code with newly implemented resistivity, we study the effect of magnetic diffusivity in the magnetospheric accretion–ejection mechanism. Physical resistivity was included in the whole computational domain so that reconnection is enabled by the physical as well as the numerical resistivity. We show, for the first time, that quasi-stationary fast ejecta of matter, which we call micro-ejections, of small mass and angular momentum fluxes, can be launched from a purely resistive magnetosphere. They are produced by a combination of pressure gradient and magnetic forces, in the presence of ongoing magnetic reconnection along the boundary layer between the star and the disk, where a current sheet is formed. The mass flux of micro-ejection increases with increasing magnetic field strength and stellar rotation rate, and is not dependent on the disk to corona density ratio and amount of resistivity.
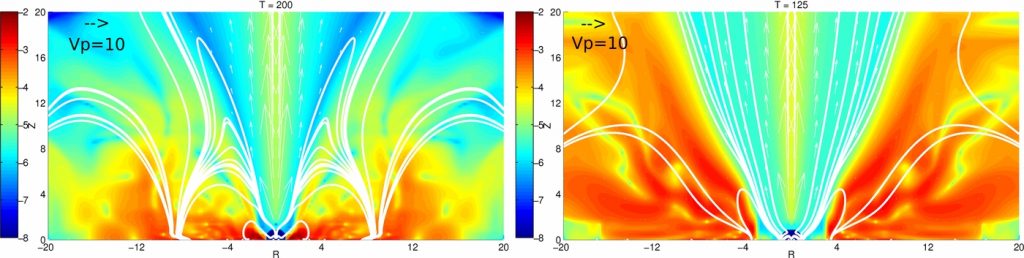
Mass flux in the presence of various magnetic field strengths
Mass flux ρv for the case with medium magnetic field is shown in the left panel, and, with larger magnetic field, in the right panel. The flow inside R < 0.5 from the axis is very fast and light, and is artificial, with a numerical origin. The mass flux is shown in a logarithmic color grading in units of Ṁ0, vectors show the velocity of matter, with vp = 10 in code units indicated in black arrow. The white solid line shows the poloidal magnetic field lines. In both plots, magnetic field lines near the axis are removed from the sample shown, in order not to obscure the underlying mass flux distribution. The disk is truncated at the radius where its ram pressure and magnetic pressure are balanced. In the left panel, this line is close to the stellar surface, so that in our resolution the disk almost touches the star. The gap is well defined in the right panel.
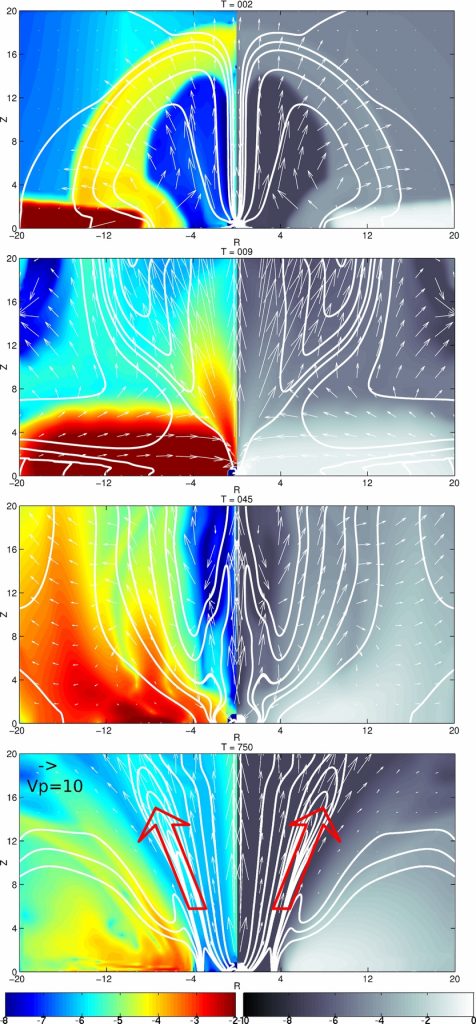
Snapshots in the fiducial simulation
The left half of each panel shows the poloidal mass flux ρvp, and the right half shows the density. The lines and arrows have the same meaning as in the above figure. Both plots are in logarithmic color scales, shown at the bottom of the panels, with the mass flux in units of Ṁ0 and the density in units of ρ0. The initial magnetic field is a pure stellar magnetic dipole, with value B* = 30 G if assumed that the disk accretion rate is 10−6 M☉ yr−1. Top to bottom are shown characteristic stages discussed in this work: (I) initial relaxation when the magnetic field is swept in and pinched near the disk mid-plane toward the star; (II) inflation and reconnection that end up opening the field, and strong infall of matter onto the star from the disk; (III) retraction of the disk matter toward the corotation radius, with a transient inflow of matter onto the star, and the light bullets of fast matter expelled along the axis—which is a numerical, artificial flow; (IV) final, quasi-stationary state, with a light, fast micro-ejection launched along the boundary layer between the stellar and the disk field. For clarity, we additionally marked micro-ejection with large red arrows.
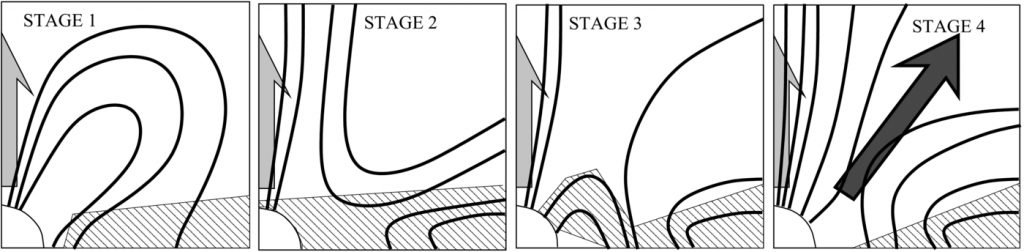
Schematic sketch of the evolution in star–disk interaction in our simulations
Stage 1: the initial stellar dipole gets pinched during the relaxation, when matter flushes in toward the central star; stage 2: the magnetic field lines are open after reconnection, and disk matter can reach the surface of the star. Our simulations here differ from most of the works in Table 1 in the violent initial conditions that bring the disk onto the star. For the setups with a stable disk, such a situation occurs only in the regime of a very weak stellar magnetic field. In the case of a strong magnetic field, configurations will be as sketched in Goodson et al. (1999), where the disk terminates in the magnetosphere, away from the star; stage 3: the disk matter retracts and a funnel flow forms from the disk inner radius and accretes matter onto the star; stage 4: the system reaches a quasi-steady state, with the magnetic field re-organized into a configuration consisting of an open stellar field and a field footed in the disk. The arrows indicate the directions of the matter flow. In the first three stages, an artificial flow of a numerical origin forms (marked with gray shadow) along the axis. It is of negligible mass flux. In the fourth stage, along the boundary between the stellar and the disk magnetic field, a micro-ejection is launched, which reaches a quasi-stationary state (marked with black shadowed arrow) together with the magnetic field.
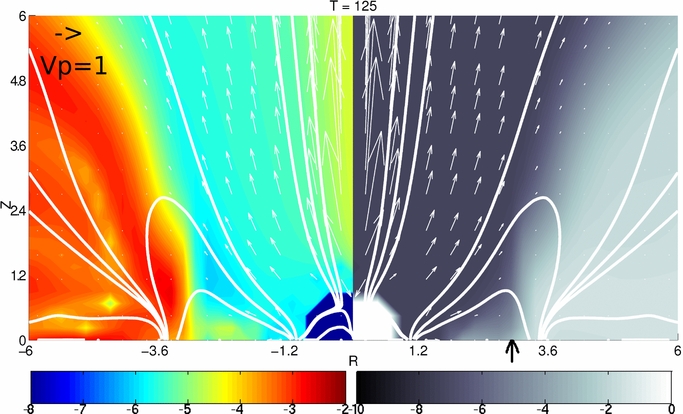
Closest vicinity of the star and the inner disk edge
Zoom into the closest vicinity of the star from to show details in the disk gap, where the disk is truncated. The left half shows mass flux and the right half shows density. The stellar magnetic field is about 200 G, for the disk mass accretion rate 10−6 M☉ yr−1. Black arrow marks the position of the truncation radius of the disk, which is in this case Rt = 3.0 R*.

